Champion-level drone racing using deep reinforcement learning - Nature
摘要
第一人称视角 (FPV) 无人机竞速是一项电视转播的运动,专业选手驾驶高速飞机穿越 3D 赛道。每位飞行员通过无人机的视角通过机载摄像头传输的视频观察周围环境。要达到专业飞行员的自主无人�机水平是一项挑战,因为机器人需要在极限范围内飞行,同时仅通过机载传感器 [^1] 估计其在赛道上的速度和位置。这里我们介绍 Swift,这是一个可以与人类世界冠军水平的实体车辆竞赛的自主系统。该系统将模拟中的深度强化学习 (RL) 与现实世界中收集的数据相结合。Swift 在现实世界的正面交锋中与三位人类冠军展开竞争,其中包括两个国际联赛的世界冠军。Swift 赢得了与每位人类冠军的几场比赛,并创下了最快的比赛时间记录。这项工作代表了移动机器人和机器智能的一个里程碑 [^2] ,这可能会启发在其他物理系统中部署基于混合学习的解决方案。
主要的
深度强化学习 [^3] 推动了人工智能的一些最新进展。使用深度强化学习训练的策略在复杂的竞技游戏中表现优于人类,包括雅达利 4、5、6 、 围棋 5、7、8、9 、 国际 象棋 5、9 、 星际 争霸 [^10] 、 Dota 2 ( 参考 文献 [^11] ) 和 Gran Turismo 12、13 。这些令人印象深刻 的机器智能能力展示主要局限于模拟和 棋盘 游戏环境,这些环境支持在精确复制测试条件中进行策略搜索。 克服这一限制并在体育竞赛中展现冠军级表现是自主移动机器人和人工智能领域长期 存在 的 问题 14、15、16 。
FPV 无人机竞赛是一项电视转播的运动,其中训练有素的人类飞行员通过高速灵活的机动将飞行器推向物理极限(图 1a )。FPV 竞赛中使用的飞行器是四轴飞行器,它们是有史以来最灵活的机器之一(图 1b )。在比赛期间,飞行器施加的力量超过其自身重量的五倍或更多,速度超过 100 km h -1 ,加速度是重力的几倍,即使在密闭空间内也是如此。每架飞行器都由一名人类飞行员远程控制,飞行员戴着耳机,耳机上显示着机载摄像头的视频流,营造出身临其境的“第一人称视角”体验(图 1c )。

图 1:无人机竞赛。
创建达到人类飞行员表现的自主系统的尝试可以追溯到 2016 年的第一届自主无人机竞赛(参考文献 [^17] ) 。随后出现了一系列创新,包括使用深度网络识别下一个门位置 18、19、20 、 将 ��竞赛 策略 从模拟转移到现实 21、22 以及 考虑感知中的不确定性 23、24。2019 年 AlphaPilot 自主无人机竞赛展示了该领域的一些最佳研究 25。 然而,前两支队伍仍然花费了几乎两倍于专业人类飞行员完成赛道的时间 26、27 。 最近 ,自主系统已经开始达到人类专家的表现 28、29、30 。然而,这些 工作依赖于外部运动捕捉系统提供的近乎 完美的状态估计。这使得与人类飞行员 的比较 不 公平,因为人类只能从无人机上获取机载观测数据。
本文将介绍 Swift,这是一个自主飞行系统,它仅使用机载传感器和计算能力,就能驾驶四旋翼飞行器与人类世界冠军进行比赛。Swift 由两个关键模块组成:(1) 感知系统,将高维视觉和惯性信息转换为低维表示;(2) 控制策略,接��收感知系统生成的低维表示并生成控制命令。
控制策略由前馈神经网络表示,并在模拟环境中使用无模型的在线策略深度强化学习 [^31] 进行训练。为了弥合模拟环境与物理世界在感知和动态方面的差异,我们利用了根据物理系统收集的数据估计的非参数经验噪声模型。这些经验噪声模型已被证明对于将控制策略从模拟环境成功迁移到现实环境至关重要。
我们在由专业无人机竞速飞手设计的实体赛道上对 Swift 进行了评估(图 1a )。赛道由七个方形门组成,体积为 30 × 30 × 8 米,形成一圈长 75 米的赛道。Swift 在这条赛道上与三位人类冠军展开角逐:2019 年无人机竞速联盟世界冠军 Alex Vanover、两届 MultiGP 国际公开赛世界杯冠军 Thomas Bitmatta 和三届瑞士全国冠军 Marvin Schaepper。Swift 和人类飞手使用的四旋翼飞行器具有相同的重量、形状和推进力。它们与国际比赛中使用的无人机类似。
人类飞行员在赛道上进行了一周的练习。练习结束后,每位飞行员将与Swift进行几场正面交锋(图 1a、b )。在每场正面交锋中,两架无人机(一架由人类飞行员控制,一架由Swift控制)从领奖台上起跑。比赛由声音信号开始。率先完成三圈完整赛道飞行,并每圈按正确顺序通过所有门的无人机将赢得比赛。
Swift 在与每位人类飞行员的比赛中都取得了胜利,并创造了赛事中最快记录。据我们所知,这是自主移动机器人首次在现实世界的竞技体育中取得世界冠军级别的成绩。
Swift 系统
Swift 结合了基于学习的算法和传统算法,将机载传感器读数映射到控制命令。该映射包含两部分:(1) 观察策略,将高维视觉和惯性信息提炼为特定于任务的低维编码;(2) 控制策略,将编码转换为无人机的指令。系统示意图如图 2 所示。
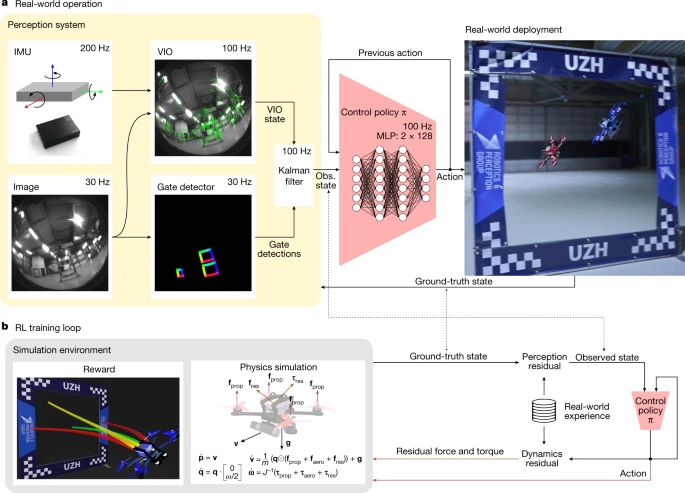
图 2:Swift 系统。
观察策略由视觉惯性估计器 32、33 组成,它们 与门检测器 26协同运行,后者是一个卷积神经网络,用于 检测 机载图像中的比赛门。检测到的门随后用于估计无人机沿赛道的全局位置和方向。这由摄像机后方交会算法 [^34] 结合赛道地图完成。然后,通过卡尔曼滤波器将从门检测器获得的全局姿态估计值与视觉惯性估计器的估计值相结合,从而更准确地表征机器人的状态。控制策略由双层感知器表示,它将卡尔曼滤波器的输出映射到无人机的控制命令。该策略在模拟中使用基于策略的无模型深度强化学习 31进行训练。在训练过程中,该策略最大化将接近下一个比赛门 [^35] 的奖励 与将下一个门保持在摄像机视野范围内的感知目标相结合的奖励。看到下一个门会得到奖励,因为它增加了姿势估计的准确性。
如果无法消除模拟与现实之间的差异,仅通过模拟来优化策略会导致物理硬件性能不佳。这些差异主要由两个因素造成:(1) 模拟动态与实际动态之间的差异;(2) 观察策略在获取真实传感数据时对机器人状态的估计存在噪声。我们通过在现实世界中收集少量数据并利用这些数据来提高模拟器的真实度,从而缓解这些差异。
具体来说,当无人机在赛道上行驶时,我们会记录机器人的机载传感器观测结果以及来自运动捕捉系统的高精度姿态估计。在此数据收集阶段,机器人由经过模拟训练的策略控制,该策略对运动捕捉系统提供的姿态估计进行操作。记录的数据可以识别通过赛道观察到的感知和动态的特征故障模式。这些感知失败和未建模动态的复杂性取决于环境、平台、赛道和传感器。感知和动态残差分别使用高斯过程 [^36] 和 k 最近邻回归建模。这种选择的动机是我们通过经验发现感知残差是随机的,而动态残差在很大程度上是确定性的(扩展数据图 1 )。这些残差模型被集成到模拟中,并且在这个增强模拟中对赛车策略进行了微调。这种方法与参考文献中用于模拟到现实转移的经验执行器模型相关。 [^37] 但进一步结合了感知系统的经验建模,并考虑了平台状态估计的随机性。
我们在扩展数据中报告的受控实验中消除了 Swift 的每个组件。此外,我们还将其与使用传统方法(包括轨迹规划和模型预测控制 (MPC))解决自主无人机竞赛任务的最新研究进行了比较。尽管此类方法在理想条件下(例如简化的动力学和对机器人状态的完美了解)实现了与我们的方法相当甚至更优的性能,但当它们的假设被违反时,它们的性能就会崩溃。我们发现依赖于预先计算路径 28、29 的 方法 对嘈杂的感知和动态特别敏感。即使配备了来自运动捕捉系统的高精度状态估计,传统方法也 无法实现与 Swift 或人类世界冠军相比具有竞争力的单圈时间。扩展数据中提供了详细的分析。
结果
无人机比赛在由外部世界级FPV飞手设计的赛道上进行。赛道上充满了各种特色动作和挑战,例如Split-S(图 1a (右上角)和 图4d )。即使发生碰撞,飞手也可以继续比赛,前提是他们的无人机仍然能够飞行。如果两架无人机都发生碰撞并无法完成比赛,则在赛道上行驶更远的无人机将获胜。
如图3b 所示 ,Swift 在与 A. Vanover 的 9 场比赛中赢了 5 场,在与 T. Bitmatta 的 7 场比赛中赢了 4 场,在与 M. Schaepper 的 9 场比赛中赢了 6 场。Swift 记录的 10 次失败中,40% 是由于与对手相撞,40% 是由于与大门相撞,20% 是由于无人机速度慢于人类飞行员。总体而言,Swift 在与每位人类飞行员的比赛中都取得了胜利。Swift 还创造了最快的比赛时间,比人类飞行员(A. Vanover)的最佳时间领先半秒。
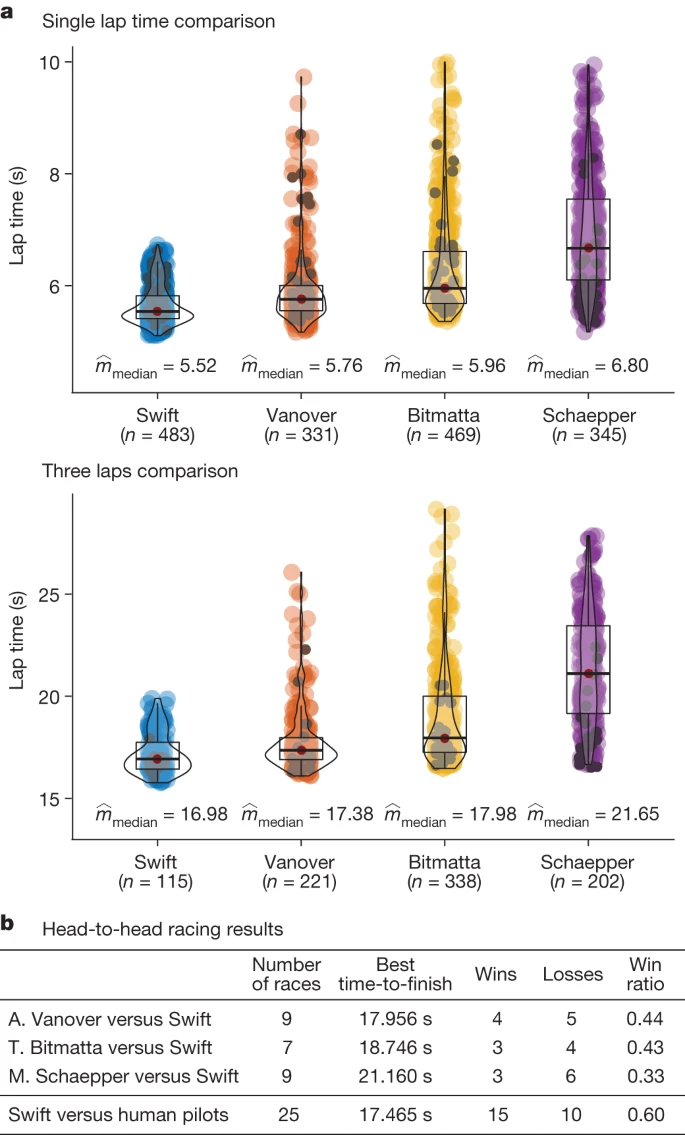
图 3:结果。
图 4 和扩展数据表 1d 对 Swift 和每位人类飞行员飞过的最快圈速进行了分析。尽管 Swift 的整体速度比所有人类飞行员都快,但它在赛道的所有单独路段上的速度并不快(扩展数据表 1 )。Swift 在起跑和急转弯(如分叉 S)时始终速度更快。起跑时,Swift 的反应时间较短,平均比人类飞行员早 120 毫秒起跑。此外,它加速更快,在进入第一个门时达到更高的速度(扩展数据表 1d ,第 1 段)。在急转弯处,如图 4c、d所示,Swift 可以找到更紧凑的动作。有一种假设是,Swift 比人类飞行员在更长的时间尺度上优化轨迹。众所周知,无模型 RL 可以通过价值函数 [^38] 优化长期奖励 。相反,人类飞行员在更短的时间尺度上规划他们的运动,最多提前一个门 [^39] 。例如在分段 S 中(图 4b、d )这一点很明显,人类飞行员在机动开始和结束时速度更快,但整体速度较慢(扩展数据表 1d ,第 3 段)。此外,人类飞行员比 Swift 更早地将飞机调整至面向下一个登机口(图 4c、d )。我们认为人类飞行员习惯于将即将到来的登机口保持在视野中,而 Swift 已经学会了依靠其他线索执行某些机动,例如惯性数据和针对周围环境特征的视觉里程计。总体而言,在整个赛道上平均而言,自主无人机实现了最高平均速度,找到了最短的赛道,并设法在整个比赛过程中将飞机保持在更接近其驱动极限的位置,如平均推力和功率所示(扩展数据表 1d )。
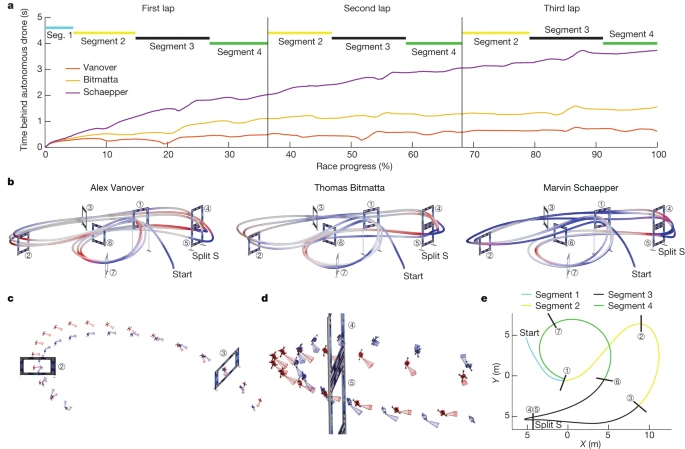
图 4:分析。
我们还比较了 Swift 和人类冠军在计时赛中的表现(图 3a )。在计时赛中,一名飞行员在赛道上比赛,圈数由飞行员自行决定。我们积累了练习周和比赛的计时赛数据,包括训练运行(图 3a ,彩色)和比赛条件下的飞行圈数(图 3a ,黑色)。对于每个参赛者,我们使用 300 多圈来计算统计数据。自主无人机更持续地追求更快的圈速,表现出更低的平均值和方差。相反,人类飞行员会根据每一圈来决定是否追求速度,无论是在训练期间还是在比赛中,都会产生更高的圈速平均值和方差。调整飞行策略的能力使人类飞行员在发现自己明显领先时可以保持较慢的速度,以降低坠机风险。自主无人机不知道它的对手,无论如何都会争取最快的预期完成时间,当领先时可能会冒太大的风险,而当落后 40 时 则风险太小。
讨论
FPV 无人机竞赛需要根据来自物理环境的嘈杂和不完整的感官输入进行实时决策。我们提出了一种自主物理系统,可以在这项运动中达到冠军级别的表现,达到甚至有时超过人类世界冠军的表现。我们的系统比人类飞行员具有某些结构优势。首先,它利用来自机载惯性测量单元 32 的 惯性数据。这类似于人类的前庭系统 [^41] ,人类飞行员并不使用该系统,因为他们并不在飞机上,也感觉不到作用在飞机上的加速度。其次,我们的系统受益于较低的感觉运动延迟(Swift 为 40 毫秒,而专业人类飞行员的平均延迟为 220 毫秒 [^39] )。另一方面,Swift 使用的摄像头的有限刷新率(30 Hz)可以被认为是人类飞行员的结构优势,他们的摄像头刷新率是人类飞行员的四倍(120 Hz),从而提高了他们的反应时间 [^42] 。
人类飞行员具有令人印象深刻的稳健性:他们可以在全速坠毁时继续飞行并完成赛道——如果硬件仍然正常工作的话。Swift 并没有接受过坠毁后恢复的训练。人类飞行员对环境条件的变化(例如照明)也具有很强的稳健性,因为环境条件的变化会显著改变赛道的外观。相比之下,Swift 的感知系统假设环境的外观与训练期间观察到的外观一致。如果不满足这个假设,系统就会失败。可以通过在多种条件下训练门检测器和残差观测模型来提供对外观变化的稳健性。解决这些限制可以使所提出的方法应用于自主无人机竞�赛中,在这种竞赛中,对环境和无人机的访问受到限制 [^25] 。
尽管仍存在诸多限制,且未来仍需进一步研究,但自主移动机器人在热门体育运动中取得世界冠军级别的成绩,无疑是机器人技术和机器智能领域的一个里程碑。这项工作或将启发基于混合学习的解决方案在其他物理系统(例如自主地面车辆、飞行器和个人机器人)中得到广泛应用。
方法
四旋翼飞行器模拟
四旋翼飞行器动力学
为了实现大规模训练,我们使用了四旋翼飞行器动力学的高保真模拟。本节简要介绍该模拟过程。飞行器的动力学可以表示为
$x˙=[p˙WBq˙WBv˙Wω˙BΩ˙]=[vWqWB⋅[0ωB/2]1m(qWB⊙(fprop+faero))+gWJ−1(τprop+τmot+τaero+τiner)1kmot(Ωss−Ω)],$
$fprop=∑ifi,τprop=∑iτi+rP,i×fi,$
(2)
$τmot=Jm+p∑iζiΩ˙i,τiner=−ωB×JωB$
(3)
$fi(Ωi)=[00cl⋅Ωi2]⊤,τi(Ωi)=[00cd⋅Ωi2]⊤$
(4)
其中 c l 和 c d 分别表示螺旋桨升力系数和阻力系数。
空气动力和扭矩
$fx∼vx+vx|vx|+Ω2¯+vxΩ2¯fy∼vy+vy|vy|+Ω2¯+vyΩ2¯fz∼vz+vz|vz|+vxy+vxy2+vxyΩ2¯+vzΩ2¯+vxyvzΩ2¯τx∼vy+vy|vy|+Ω2¯+vyΩ2¯+vy|vy|Ω2¯τy∼vx+vx|vx|+Ω2¯+vxΩ2¯+vx|vx|Ω2¯τz∼vx+vy$
然后,我们会从真实飞行数据中识别相应的系数,并使用运动捕捉技术提供地面实况力和扭矩测量值。我们使用来自赛道的数据,使动力学模型能够拟合赛道。这类似于人类飞行员在比赛前几天或几周在特定赛道上进行的训练。在我们的案例中,人类飞行员会在比赛前在同一赛道上进行为期一周的练习。
Betaflight 低级控制器
为了控制四旋翼飞行器,神经网络输出总推力和机身速率。众所周知,这种控制信号兼具高灵活性和良好的鲁棒性,易于从模拟转换到现实 [^44] 。然后,预测的总推力和机身速率由机载低级控制器处理,该控制器计算各个电机指令,随后通过控制电机的电子速度控制器 (ESC) 将这些指令转换成模拟电压信号。在实体飞行器上,这种低级比例-积分-微分 (PID) 控制器和 ESC 是使用开源 Betaflight 和 BLHeli32 固件 [^45] 实现的。在模拟中,我们使用低级控制器和电机速度控制器的精确模型。
由于 Betaflight PID 控制器已针对载人飞行进行了优化,因此它表现出一些特性,而仿真能够准确捕捉这些特性:D 项的参考值始终为零(纯阻尼),I 项在油门关闭时重置,并且在电机推力饱和的情况下,机身速率控制被赋予优先级(按比例缩小所有电机信号以避免饱和)。用于仿真的控制器增益已从 Betaflight 控制器内部状态的详细日志中识别出来。仿真能够预测各个电机指令,误差小于 1%。
电池模型和ESC
底层控制器将各个电机指令转换为脉冲宽度调制 (PWM) 信号,并将其发送至控制电机的 ESC。由于 ESC 不对电机转速进行闭环控制,因此 给定 PWM 电机指令 cmd i时,稳态电机转速 Ω i,ss是电池电压的函数。因此,我们的仿真使用灰盒电池模型 [^46] 对电池电压进行建模, 该模型基于瞬时功耗 P mot 来模拟电压:
$Pmot=cdΩ3η$
(5)
然后, 电池模型 [^46] 根据该功率需求模拟电池电压。给定电池电压 Ubat 和单个电机指令 ucmd , i ,我们使用映射(同样省略了与每个加数相乘的系数)
$Ωi,ss∼1+Ubat+ucmd,i+ucmd,i+Ubatucmd,i$
(6)
计算公式 ( 1 )中动力学仿真所需的 相应稳态电机转速 Ω i,ss 。这些系数已从包含所有相关量测量值的 Betaflight 日志中识别出来。结合低级控制器模型,这使得模拟器能够将总推力和机体速率形式的动作正确地转换为 公式 ( 1 ) 中所需的电机转速 Ω ss 。
策略训练
我们训练深度神经控制策略,将 平台状态和下一个门控观测值的观测值 o t直接映射到质量归一化集体推力和身体速率 [^44] 形式的控制动作 u t 。控制策略在模拟中使用无模型强化学习进行训练。
训练算法
训练使用近端策略优化31 进行 。这种“演员-评论家”方法需要在训练期间联合优化两个神经网络:策略网络(将观察结果映射到动作)和价值网络(充当“评论家”并评估策略所采取的动作)。训练结束后,只需在机器人上部署策略网络。
观察、行动和奖励
$rt=rtprog+rtperc+rtcmd−rtcrash$
(7)
其中, r prog 奖励朝着下一个门 [^35] 前进; r perc 编码感知意识,通过调整车辆姿态使摄像头的光轴指向下一个门的中心; r cmd 奖励平稳动作; r crash 是一个二元惩罚,仅在与门碰撞或平台离开预定义边界框时生效。如果 r crash 被触发,则训练过程结束。
具体来说,奖励条款如下
$rtprog=λ1[dt−1Gate−dtGate]rtperc=λ2exp[λ3⋅δcam4]$
(8)
$rtcmd=λ4atω+λ5∥at−at−1∥2$
(9)
训练详情
数据收集是通过模拟 100 个代理并行执行的,这些代理以 1,500 步为一集与环境交互。在每次环境重置时,每个代理都在轨道上的一个随机门处初始化,并在通过此门时围绕先前观察到的状态产生有界扰动。与以前的工作 44、49、50 不同 , 我们 在 训练 时 不对平台动态进行随机化。相反,我们根据真实数据进行微调。训练环境是使用 TensorFlow Agents [^51] 实现的。策略网络和价值网络均由两层感知器表示,每层有 128 个节点,LeakyReLU 激活具有负斜率为 0.2。使用 Adam 优化器优化网络参数, 策略网络和价值网络的学习率均为3 × 10 −4 。
策略训练总共涉及 1 × 10 8 个 环境交互,在工作站(i9 12900K、RTX 3090、32 GB RAM DDR5)上耗时 50 分钟。微调涉及 2 × 10 7 个 环境交互。
残差模型辨识
我们基于在现实世界中收集的少量数据对原始策略进行微调。具体来说,我们在现实世界中收集了三次完整的rollout数据,相当于大约50秒的飞行时间。我们通过识别残差观测值和残差动态来微调策略,并将其用于模拟训练。在此微调阶段,仅更新控制策略的权重,而门检测网络的权重保持不变。
残差观测模型
高速导航会导致严重的运动模糊,这可能导致追踪的视觉特征丢失,并导致线性里程计估计值出现严重漂移。我们使用一个里程计模型来微调策略,该模型仅从现实世界中记录的少量试验中识别出来。为了�对里程计中的漂移进行建模,我们使用高斯过程 [^36] ,因为它们可以拟合里程计扰动的后验分布,从而我们可以从中采样时间一致的实现。
具体来说,高斯过程模型将残差位置、速度和姿态拟合为机器人地面真实状态的函数。观测残差的识别是通过比较真实世界滚动过程中观察到的视觉惯性里程计 (VIO) 估计值与从外部运动跟踪系统获得的地面真实平台状态来实现的。
我们分别处理观测值的每个维度,有效地将一组九个一维高斯过程拟合到观测残差中。我们使用混合径向基函数核
$κ(zi,zj)=σf2exp(−12(zi−zj)⊤L−2(zi−zj))+σn2$
(10)
其中 L 是对角长度尺度矩阵, σ f 和 σ n 分别表示数据和先验噪声方差, z i 和 z j 表示数据特征。通过最大化对数边际似然来优化核超参数。核超参数优化后,我们从后验分布中采样新的实现,然后用于策略的微调。扩展数据图 1 展示了实际部署中位置、速度和姿态的残差观测值,以及从高斯过程模型中采样的 100 个实现。
残差动力学模型
我们使用残差模型来补充模拟的机器人动力学 [^52] 。具体来说,我们将残差加速度确定为平台状态 s 和指令质量归一化总推力 c 的函数:
$ares=KNN(s,c)$
(11)
我们使用 k = 5 的 k 最近邻回归。 用于残差动力学模型识别的数据集的大小取决于轨道布局,对于本研究中使用的轨道布局,范围在 800 到 1,000 个样本之间。
门检测
为了校正 VIO 管道累积的漂移,门被用作相对定位的不同地标。具体来说,通过分割门角 [^26] 在机载摄像头视图中检测门。英特尔实感追踪摄像头 T265 提供的灰度图像用作门检测器的输入图像。分割网络的架构是一个六级 U-Net [^53] ,每级有 (8, 16, 16, 16, 16) 个大小为 (3, 3, 3, 5, 7, 7) 的卷积滤波器,最后一个额外层对包含 12 个滤波器的 U-Net 的输出进行操作。使用 α = 0.01 的 LeakyReLU 作为激活函数。为了在 NVIDIA Jetson TX2 上部署,该网络被移植到 TensorRT。为了优化内存占用和计算时间,推理以半精度模式(FP16)进行,图像在输入网络之前会被下采样至 384 × 384 的尺寸。在 NVIDIA Jetson TX2 上,一次前向传递需要 40 毫秒。
VIO漂移估计
来自 VIO 管道 54 的 里程计估计值在高速飞行过程中会出现明显的漂移。我们使用门检测来稳定 VIO 产生的姿态估计值�。门检测器输出所有可见门的角点坐标。首先使用基于无穷小平面的姿态估计 (IPPE) [^34] 为所有预测门估计一个相对姿态。根据这个相对姿态估计值,将每个门观测值分配给已知轨迹布局中最近的门,从而得到无人机的姿态估计值。
状态 x 和协方差 P 更新由下式给出:
$xk+1=Fxk,Pk+1=FPkF⊤+Q,$
(12)
$F=[I3×3dtI3×303×3I3×3],Q=[σposI3×303×303×3σvelI3×3].$
(13)
$Kk=Pk−Hk⊤(HkPk−Hk⊤+R)−1,xk+=xk−+Kk(zk−H(xk−)),Pk+=(I−KkHk)Pk−,$
(14)
其中 Kk 是卡尔曼增益, R 是 测量协方差, Hk 是 测量矩阵。如果在单个摄像机帧中检测到多个门,则所有相对姿态估计都会被堆叠并在同一个卡尔曼滤波器更新步骤中处理。测量误差的主要来源是网络门角检测的不确定性。当应用 IPPE 时,图像平面中的这个误差会导致姿态误差。我们选择了一种基于采样的方法,从已知的平均门角检测不确定性中估计姿态误差。对于每个门,IPPE 算法应用于标称门观测以及 20 个扰动门角估计。然后使用所得的姿态估计分布来近似 门观测的测量协方差 R。
模拟结果
在自主无人机竞赛中要达到冠军级的表现需要克服两个挑战:不完善的感知和不完整的系统动态模型。在模拟的受控实验中,我们评估了我们的方法对这两个挑战的稳健性。为此,我们评估了在四种不同设置下部署时在竞赛任务中的表现。在设置 (1) 中,我们模拟了一个简单的四旋��翼模型,可以访问地面真实状态观测值。在设置 (2) 中,我们用从真实飞行中识别出的噪声观测值替换地面真实状态观测值。这些噪声观测值是通过从残差观测模型中采样一个实现生成的,并且与部署的控制器的感知意识无关。设置 (3) 和 (4) 分别与前两个设置共享观测模型,但用更精确的空气动力学模拟 [^43] 取代了简单的动力学模型。这四种设置允许对方法对动态变化和观测保真度的敏感性进行受控评估。
在这四种设置中,我们都根据以下基线对我们的方法进行基准测试:零样本、域随机化和时间最优。零样本基线表示使用无模型 RL 训练的基于学习的竞赛策略 [^35] ,该策略从训练域零样本部署到测试域。该策略的训练域等于实验设置 (1),即理想化的动态和地面真实观测。域随机化通过随机化观测和动态属性来扩展零样本基线的学习策略,以提高鲁棒性。时间最优基线使用预先计算的时间最优轨迹 28 ,使用 MPC 控制器进行跟踪。与其他基于模型的时间最优飞行方法 55、56 相比 , 此方法表现出最佳性能 。轨迹生成和 MPC 控制器使用的动态模型与实验设置 (1) 的模拟动态相匹配。
性能评估通过评估最快单圈时间、成功通过闸门的平均和最小观测距离以及成功完成的航迹百分比来体现。闸门距离指标衡量无人机通过闸门平面时与闸门上最近点之间的距离。闸门距离较大表示四旋翼飞行器通过时靠近闸门中心。较小的闸门距离可以提高速度,但也会增加碰撞或错过闸门的风险。任何导致碰撞的单圈均不视为有效。
结果总结在扩展数据表 1c 中。所有方法在理想化的动态和地面实况观测中部署时都能成功完成任务,其中时间最优的基线产生最低的单圈时间。当部署在具有域转移的设置中时,无论是在动态还是观测中,所有基线的性能都会崩溃,并且三个基线都无法完成哪怕一圈。这种性能下降在基于学习的方法和传统方法中都有所表现。相比之下,我们的方法以动态和观测噪声的经验模型为特色,在所有部署设置中都取得了成功,单圈时间略有增加。
我们的方法之所以能够在各种部署机制中取得成功,关键在于它使用了基于真实数据估算的动态和观测噪声经验模型。将能够访问此类数据的方法与无法访问此类数据的方法进行比较并不完全公平。因此,我们还在访问与我们的方法相同的真实数据时,对所有基线方法的性能进行了基准测试。具体而言,我们比较了实验环境 (2) 下的性能,该环境采用理想化的动态模型,但感知存在噪声。所有基线方法都提供了我们用来表征观测噪声的相同高斯过程模型的预测值。�结果总结在扩展数据表 1b 中。所有基线方法都受益于更真实的观测,从而获得了更高的完成率。然而,我们的方法是唯一能够可靠地完成整个轨迹的方法。除了观测噪声模型的预测之外,我们的方法还考虑了模型的不确定性。有关强化学习与最优控制在受控实验中的性能的深入比较,请参阅参考文献 [^57] 。
经过多次迭代进行微调
我们研究了迭代过程中行为变化的程度。分析结果表明,后续的微调操作对性能的提升和行为的改变几乎可以忽略不计(扩展数据图 2 )。
接下来,我们将提供有关此调查的更多细节。我们首先列举微调步骤,以提供必要的符号:
- 在模拟中训练策略 0。
- 在现实世界中部署策略 0。该策略基于来自运动捕捉系统的真实数据运行。
- 识别现实世界中策略 0 观察到的残差。
- 通过对已识别的残差微调策略 0 来训练策略 1。
- 在现实世界中部署策略 1。该策略仅对机载传感测量数据起作用。
- 识别现实世界中策略 1 观察到的残差。
- 通过对已识别的残差进行策略 1 的微调来训练策略 2。
我们在对各自的残差进行微调后,在模拟中比较了策略 1 和策略 2 的性能。结果如扩展数据图 2 所示。我们观察到,与门中心的距离差异(该距离是衡量策略安全性的指标)为 0.09 ± 0.08 米。此外,完成一圈所需时间的差异为 0.02 ± 0.02 秒。请注意,这个单圈时间差异远远小于 Swift 和人类飞行员的单圈完成时间差异(0.16 秒)。
无人机硬件配置
人类飞行员和 Swift 使用的四旋翼飞行器具有相同的重量、形状和推进力。平台设计基于 Agilicious 框架 58。 每辆车的重量为 870 克,可以产生大约 35 N 的最大静态推力,从而使静态推重比为 4.1。每个平台的底座由一个 Armattan Chameleon 6 英寸主机架组成,该主机架配备 T-Motor Velox 2306 电机和 5 英寸三叶螺旋桨。配备 Connect Tech Quasar 载板的 NVIDIA Jetson TX2 为自主无人机提供主要计算资源,具有运行速度为 2 GHz 的六核 CPU 和一个运行速度为 1.3 GHz 的具有 256 个 CUDA 核心的专用 GPU。虽然门检测网络的前向传递是在 GPU 上执行的,但竞赛策略是在 CPU 上评估的,一次推理传递需要 8 毫秒。自动无人机搭载英特尔 RealSense 追踪摄像头 T265,可提供 100 Hz 的 VIO 估计值 [^59] ,并通过 USB 传输至 NVIDIA Jetson TX2。载人无人机既不搭载 Jetson 计算机,也不搭载 RealSense 摄像头,而是配备了相应的压载物。由人类飞行员或 Swift 产生的总推力和机身速率等控制指令被发送到商用飞行控制器,该控制器基于 216 MHz 的 STM32 处理器运行。飞行控制器运行 Betaflight,这是一款开源飞行控制软件 [^45] 。
人类飞行员的印象
以下引言传达了与 Swift 比赛的三位人类冠军的印象。
亚历克斯·瓦诺弗 :
- 这些比赛将在 S 分段决出胜负,这是赛道上最具挑战性的部分。
- 这真是一场精彩的比赛!我离自主飞行的无人机太近了,以至于在努力跟上它的时候,我都能感觉到气流的冲击。
托马斯·比特马塔 :
- 可能性无穷无尽,这是一个可能改变整个世界的开始。另一方面,我是个赛车手,我不希望任何东西比我更快。
- 随着飞行速度的加快,您需要牺牲精度来换取速度。
- 无人机的潜力令人振奋。很快,人工智能无人机甚至可以用作训练工具,帮助人们了解其未来的可能性。
马文·谢珀 :
- 与机器比赛的感觉很不一样,因为你知道机器不会累。
研究伦理
本研究遵循《赫尔辛基宣言》进行。根据苏黎世大学的规章制度,由于未收集任何健康相关数据,本研究方案无需接受伦理委员会审查。受试者在参与研究前已签署书面知情同意书。
数据可用性
评估��本文结论所需的所有其他数据均包含在论文或扩展数据中。赛事的动作捕捉记录及其分析代码可在 Zenodo 的“racing_data.zip”文件中找到,网址为 https://doi.org/10.5281/zenodo.7955278 。
代码可用性
详细说明训练过程和算法的 Swift 伪代码可在 Zenodo 的“pseudocode.zip”文件中找到,网址为 https://doi.org/10.5281/zenodo.7955278 。为防止潜在的滥用,与本研究相关的完整源代码将不会公开。